The methods in this category overlap with unsupervised learning methods for anomaly detection because unsupervised methods assume that normal data samples are much more than anomalous samples. Therefore, this type of method is more suitable for datasets predominated by normal data. Brief information will be provided in the following for several popular methods in this category. Then much more details will be provided for one of the most useful anomaly detection methods: autoencoder (or AutoEncoder).

Some common methods in this category are one-class SVM, SVDD, GMM, Naive Bayes, and AutoEncoder [143]. One-class SVM uses kernel functions to map data to a higher-dimensional space. Then in such space, hyperplanes will be sought to achieve the maximum distance between the data and the origin. SVDD also uses kernel functions to map data to a higher-dimensional space. Then, the smallest sphere that can contain all the normal data points is sought. GMM uses normal data samples to build a model via the maximum likelihood estimation. Then this trained model evaluates samples for anomaly detection for their probability of belonging to normal data. Naive Bayes is performed in a way similar to GMM. The model trained with normal data can give out the probability of new samples belonging to the normal data category. Autoencoder trains the data through a sequential encoder and decoder process to filter out less significant attributes. Samples whose decoding results are much different from the original sample will be determined as an anomaly.

Autoencoder uses a special type of artificial neural network to attract essential information from data [144]. Thus, it can be used to learn a representation (encoding) for a set of data, typically for dimensionality reduction, by training the network to ignore insignificant data ("noise"). For this purpose, we use the encoder to attract the essential information and use a decoder to convert the data with only the essential information back. In this process, as illustrated in Fig. 13.5, if the
autoencoder is trained with normal data, then this trained model can retain the characteristics essential to all the normal data, and the samples that go through the process will be close to the original data. Due to the same reason, anomalies that go through such a process will generate results that are much different from the normal data.

Figure 13.5: Illustration of autoencoder
Distinct from PCA, the autoencoder gains a nonlinearity capability attributed to the use of ANNs, which helps better extract the major attributes of the normal data. This will help identify anomalies in problems with nonlinearity.

The remaining of this subsection presents code for a simple demonstration of using autoencoder for anomaly detection. In the code, an autoencoder was constructed with a simple deep neural network consisting of two parts for encoding and decoding. The MNIST dataset consisting of 50000 training samples and 10000 testing samples were adopted. The autoencoder was trained with the training data. 100 images out of the testing dataset were modified with random noise to serve as anomalies. The testing data was used for predictions, for which the error was obtained in terms of the sum of square root errors for each image. It can be seen that errors in the normal data and anomalies in the predicted results are much different. This indicates that the autoencoder can be used to identify the anomalies easily in this example.

First, we imported all the needed packages. A random seed was set to ensure that we would get the same results every time despite the use of random numbers.

import numpy as np
              from keras.datasets import mnist
              import ssl
              ssl._create_default_https_context = ssl._create_unverified_context
              from keras.models import Model
              from keras.layers import Dense, Input
              import matplotlib.pyplot as plt
              np.random.seed(9527) # for reproducibility
              

The MNIST dataset was imported. Then we recorded the shape of the original image for later use, which is needed because the images have to be flattened for the deep NN. 100 anomalous samples were created by randomly selecting 100 samples out of the 10000 testing samples and then adding noise defined by a normal distribution with a mean of 0 and a standard variation of 40 . Next, the data was scaled into the range between 0 and 1 , which was needed for deep learning to ensure good training results and facilitate result evaluation.

# Load data
              (x_train, _), (x_test, y_test) = mnist.load_data()
              image_shape = x_train[0].shape # original image shape
              # Create 100 anomalous samples (outliners) in testing data
              outlier_index = np.random.randint(0,x_test.shape[0], size=100)
              x_test[outlier_index] = x_test[outlier_index] + np.random.normal(0, 40, image_shape)
              # Data preprocessing: scaling and reshaping
              x_train = x_train.astype('float32') / 255. # minmax_normalized
              x_test = x_test.astype('float 32') / 255. # minmax_normalized
              

x_train = x_train.reshape((x_train.shape[0], -1))
              x_test = x_test.reshape((x_test.shape[0], -1))
              

The autoencoder model was created using deep NN. As can be seen in the following code, the NN was built layer by layer. The NN has a symmetric structure for the two parts: encoding and decoding.

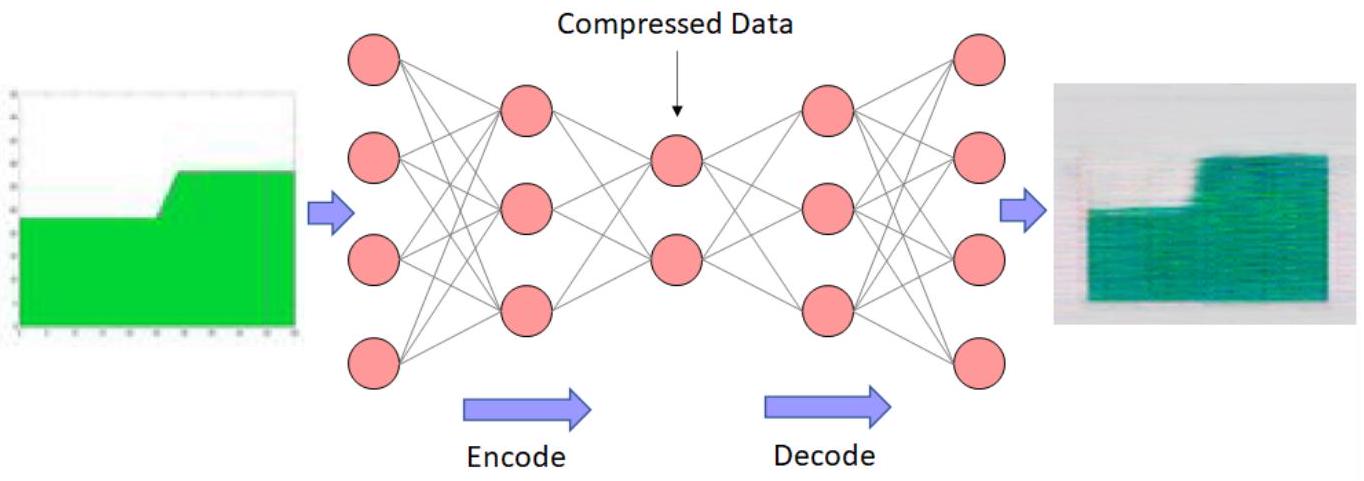
# Built Autoencoder
              input_img = Input(shape=(x_train.shape[-1],))
              # Encoding
              encoded = Dense(24, activation='relu')(input_img)
              encoded = Dense(12, activation='relu')(encoded)
              encoded = Dense(8, activation='relu') (encoded)
              encoder_output = Dense(4)(encoded)
              # Decoding
              decoded = Dense(8, activation='relu')(encoder_output)
              decoded = Dense(12, activation='relu')(decoded)
              decoded = Dense(24, activation='relu')(decoded)
              decoded = Dense(x_train.shape[-1])(decoded)
              # Build autoencoder NN model
              autoencoder = Model(inputs=input_img, outputs=decoded)
              # Compile autoencoder
              autoencoder.compile(loss='mse', optimizer='adam')
              

Then, we first trained the model with the training data. Next, predictions were performed with testing data, which contains the anomalies.

# Training
              autoencoder.fit(x_train, x_train, epochs=20, batch_size=30, shuffle=True)
              # Prediction
              autoencoded_imgs = autoencoder.predict(x_test)
              

The original data ("x_test") and the decoded data ("autoencoded_imgs") were compared to obtain the error. Then we split the data into normal samples and anomalies for plotting.

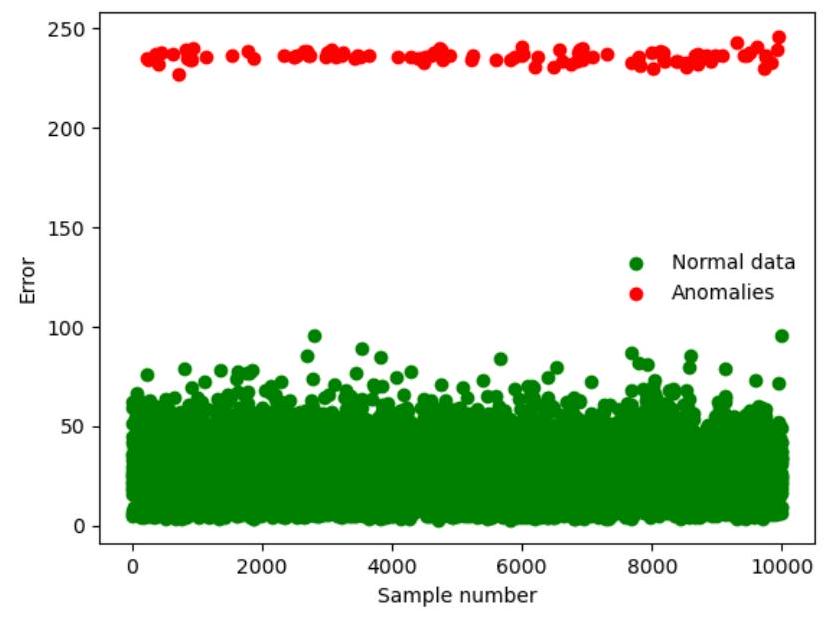
Error = np.sum((x_test-autoencoded_imgs)**2,axis=1) # Sum of squre root errors
              Normal_data = np.delete(Error,outlier_index) # Normal data
              Outliners = Error[outlier_index] # Anomalies
              plt.scatter(np.delete(np.arange(Error.size),outlier_index),Normal_data,c=' g',label='Normal data')
              plt.scatter(outlier_index,Error[outlier_index], c='r', label='Anomalies')
              plt.legend(loc="middle right",fontsize=10,frameon=False)
              plt.xlabel('Sample number')
              plt.ylabel('Error')
              

As shown in Fig. 13.6, the errors or anomalies are much different from those of the normal samples. Thus, when new data that is much different from the normal data (used for training this autoencoder model) is processed, the autoencoder will tend to give significantly different results. These differences can be used to differentiate anomalies from normal data.

Data quality is critical to the anomaly detection practice. In particular, the selection of anomaly detection algorithms relies on the nature and quality of the data. This is because the data, to a great extent, defines what anomaly detection problem to address. The quality of the dataset is a major driver in developing accurate and usable anomaly detection models.

Common data quality issues in anomaly detection applications are listed below:

Figure 13.6: Results for using autoencoder for anomaly detection

Common useful practices for addressing the above data quality issues in anomaly detection include but are not limited to the following ones.

The imbalanced distribution of the samples is a common issue in anomaly detection. This issue is especially obvious when we use classification algorithms with labeled data for anomaly detection, which can easily suffer from the class imbalance issue. For example, when the training set contains a very small number of anomaly samples, the classification model may yield very good accuracy. However, such a model may still be useless because the accuracy is primarily contributed by the predominant normal samples while the model's consideration of anomalies may be far from adequate.

Such issues can be addressed from different angles including data, model, and model evaluation metrics.